100次浏览 发布时间：2024-09-14 09:04:23
角是几何图形中最重要的元素，证明两直线位置关系、运用全等三角形、相似三角形都要涉及角，而圆的特征，赋予角极强的活性，使得角能灵活地互相转化．
与圆有关的角：
1、圆心角：顶点在圆心的角叫做圆心角。
2、圆周角：顶点在圆上，两条边都和圆相交的角叫做圆周角．
圆周角定理：一条弧所对的圆周角等于它所对的圆心角的一半．
※3、弦切角：顶点在圆上，一条边和圆相交，另一条边和圆相切的角叫做弦切角．
弦切角定理：弦切角等于它所夹的弧所对的圆周角．
根据圆心角与圆周角的倍半关系，可实现圆心角与圆周角的转化；由同弧或等弧所对的圆周角相等，可将圆周角在大小不变的情况下，改变顶点在圆上的位置进行探索；由圆内接四边形的对角互补和外角等于内对角，可将与圆有关的角互相联系起来．
熟悉以下基本图形
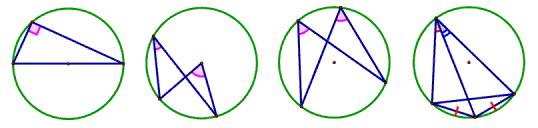
注：（1）弧是联系与圆有关的角的中介，“由弧到角，由角看弧”是促使与圆有关的角相互转化的基本方法．
（2）构造直径上90°的圆周角，是解与圆相关问题的常用辅助线，这样就为勾股定理的运用、相似三角形的判定创造了条件．
【问题解决】
直线AB与⊙O相交于A，B两点，点C在⊙O上，且∠BOC=40°，点E是直线AB上一个动点（与点O不重合），直线EC交⊙O于另一点D，则使DE=DO的点总共有 个．
【思路分析】
作出图形，分类讨论.根据画图可知应分E在BA的延长线上、在线段AB上、在AB的延长线上三种情况来解决．
【图文解析】（观察动态演示）
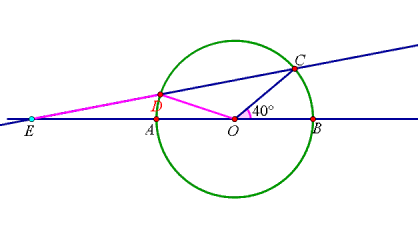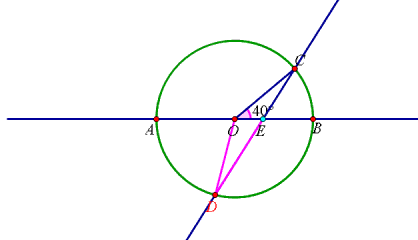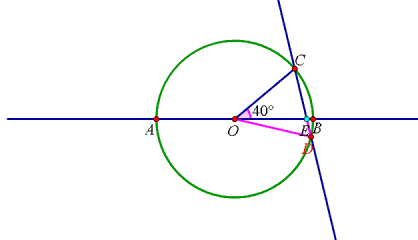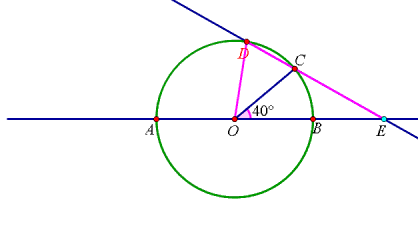
当点E在BA的延长线上，如图：
设∠CEO=x°，
∵DE=DO，
∴∠DOE=∠CEO=x°，
∵OC=OD，
∴∠OCD=∠ODC=2x°，
∵∠BOC=∠OCD+∠CEO，
∴2x+x=40，
当点E在线段AB上，如图：
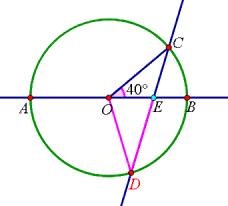
设∠CDO=x°，
∵OC=OD，
∴∠OCD=∠ODC=x°，
∵DE=DO，
∴∠DOE=∠DEO=（40+x）°，
由三角形内角和定理得：x+40+x+40+x=180，
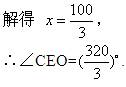
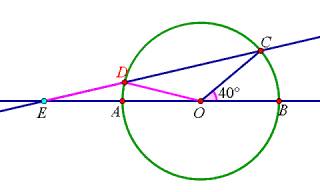
当点E在AB的延长线上，如图：
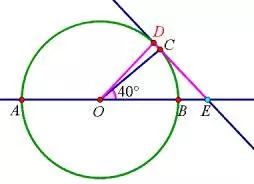
设∠CEO=x°，
∵DE=DO，
∴∠DOE=∠CEO=x°，∠COD=（x-40）°
∵OC=OD，
∴∠ODC=∠OCD=（40+x）°，
由三角形内角和定理得：x-40+2（40+x）=180，
故答案为3.
【点评】本题考查了圆心角、弧、弦的关系以及圆周角定理，根据等腰三角形的性质和三角形的内角和定理即可得到三种情况.正确画出图形，灵活转化圆中角是解决本题的关键。
探究乐园：
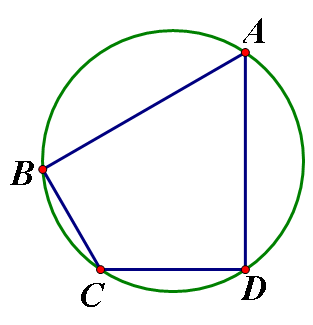
1、如图，圆内接四边形ABCD中，∠A=60°，∠B=90°，AD=3，CD=2，则BC= .
2、如图，ABCD是⊙O的内接四边形，延长BC到E，已知∠BCD：∠ECD=3：2，那么∠BOD= °.
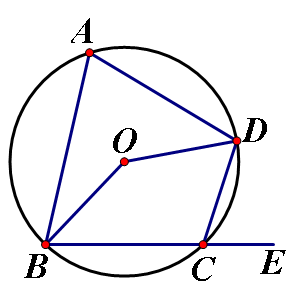
3、如图，已知四边形ABCD外接⊙O的的半径为5，对角线AC与BD的交点为E，且AB²=AE×AC，BD=8，求△ABD的面积.
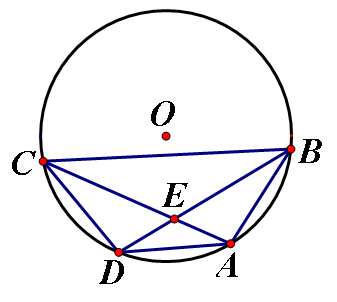
4、如图，已知AD是△ABC外角∠EAC的平分线，交BC的延长线于点D，延长DA交△ABC的外接圆于点F，连结FB、FC.
（1）求证：FB=FC；
（2）求证：FB²=FA×FD；
（3）若AB是△ABC的外接圆的直径，∠EAC=120°，BC=6cm，求AD的长.
英国集宝保险柜售后服务热线及其服务网点介绍
英国集宝保险柜：400-883-2086，一键呼叫，服务到家——让您的英国集宝保险柜明心之所向，践专注之行。我们深知您的英国集宝保险柜电器对您意义非凡，因此我们提供全方位的，让您的英国集宝保险柜在使用中随时享受如家的呵护：英国集宝保险柜 售后，您专属的英国集宝保险柜 服务团队，全天候技术支持
2025-04-02 09:33:18
操盘必读丨首饰金价已接近千元心理线；4月5日起国内机票燃油附加费下调
要闻精选＞＞王毅谈中美贸易战：若美继续搞各种讹诈 中方必将坚决反制当地时间4月1日，中共中央政治局委员、外交部长王毅接受采访时表示，“美国优先”不应是美式霸凌，更不能把自己的利益建立在损害别国正当权益的基础之上。中国从来不接受强权霸权，美方如果一味施压，甚至继续搞各种讹诈，中方必将坚决反制。王毅表示
2025-04-02 09:30:00
中旗新材市场竞争加剧净利三年降77% 贺荣明8亿入局成新实控人股价涨停
长江商报消息 ●长江商报记者 徐佳上市不到4年的中旗新材（001212.SZ）将易主。3月31日晚间，中旗新材披露实控权变动。广东星空科技装备有限公司（以下简称“星空科技”）拟受让中旗新材控股股东、实控人等持有的公司股份3049.89万股，占上市公司股份总数的24.97%；星空科技的一致行动人陈耀民
2025-04-02 09:28:00
方宬保险柜售后服务维修热线
方宬保险柜24小时售后客服中心：400-883-2086方宬保险柜，作为一家资深且信誉卓著的服务提供商，自成立以来便专注于为各界客户提供安全可靠的产品质量与维护解决方案。我们不仅拥有完备的工商注册资质，并且每一项服务均经过相关单位严格备案，确保每一次上门服务既专业又合法，给予客户十足的安全感
2025-04-02 09:27:14
鹤彩保险柜全国各市售后服务热线号码
鹤彩保险柜售后服务电话：400-883-2086鹤彩保险柜24小时客服热线：400-883-2086鹤彩保险柜24小时人工客服、线下专业全国网点及各地区 专业人员服务团队等专属服务，整个报修流程规范有序，后期同步跟踪查询公开透明。所有专业团队均经过专业培训、持证上岗，所用配件均为原厂直供
2025-04-02 09:21:13